主専攻実験概要

　　　　Experiment

9. ３次元位置計測センサ

視点移動に応じたインタラクティブな映像を生成するための３次元位置計測センサの使用方法について学習します。
仮想空間の中で運動視差の効果を利用したインタラクティブな映像体験を実現するには、利用者の視点位置に応じた映像生成を行う必要があります。ここでは、利用者の視点位置を計測するためのセンサとして、磁気センサFlock of Birdsを使用し、３次元位置計測センサの使用方法を学びます。

9.1 磁気センサ

本実験では、３次元空間における位置計測のためのセンサとして、Ascension Technology Corporation社の磁気センサFlock of Birdsを使用します。磁気センサは非接触で空間内の位置を測定することができるため、多くのVRシステムで使用されています。

磁気センサは磁界を発生するトランスミッタと、磁界の変化を受けるレシーバから構成されています。トランスミッタ、レシーバはそれぞれ３方向の直交コイルで構成されており、トランスミッタの３つのコイルを順に励磁すると、レシーバの３つのコイルには順次、起電力が発生します。このレシーバの各コイルの起電力を計測することで、トランスミッタに対するレシーバの相対的な位置（x, y, z）と角度（azimuth, elevation, roll）の6自由度の情報を得ることができます。

　　　
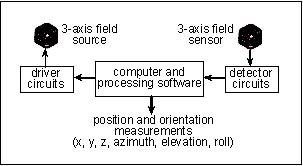
　　　　図9.1：Flock of Birdsの概観　　　　　　　　　　　　　　　図9.2：磁気センサの位置計測原理
Flock of Birdsの主な仕様は、以下の通りです。
-測定自由度　：　6DOF　(x, y, z, azimuth, elevation, roll)
-精度　　　　：　位置1.8mmRMS、角度0.5度RMS
-解像度　　　：　位置0.5mm、角度0.1度
-測定範囲　　：　半径約1.2m
-データレート　：　最大144Hz
-インタフェース：　シリアル（RS-232C）接続
Flock of Birdsに関する詳しい情報は以下を参照して下さい。
・http://www.ascension-tech.com/products/flockofbirds.php

　
9.2 座標変換

磁気センサFlock of Birdsから取得されるデータは、センサ固有の座標系（Xs, Ys, Zs）で表されています。このデータを仮想世界の中で使用するためには、仮想空間のワールド座標系（Xw, Yw, Zw）に変換して使用する必要があります。
下の図は、Flock of Birdsのトランスミッタの設置によるセンサ座標系の方向を示したものです。仮想世界のワールド座標系は、スクリーンに向かって図のように、Xw（右）、Yw（前）、Zw（上）の方向を取ります。これに対し、例えば下図のようにトランスミッタを置いた場合、ワールド座標系とセンサ座標系で座標軸の方向が異なるため、次式のように座標変換を行います。この際、センサの計測データはinchの単位系で取得されるのに対し、ワールド座標系ではmの単位系で表すことにします。
　　Xw = 0.0254*Xs+X0
　　Yw = -0.0254*Ys+Y0
　　Zw = -0.0254*Zs+Z0
（Xs, Ys, Zs）はセンサの計測データ（センサ座標系で表されたレシーバの相対位置座標）、（X0, Y0, Z0）は、ワールド座標系でのトランスミッタの位置座標、（Xw, Yw, Zw）はワールド座標系に変換されたレシーバの位置座標です。

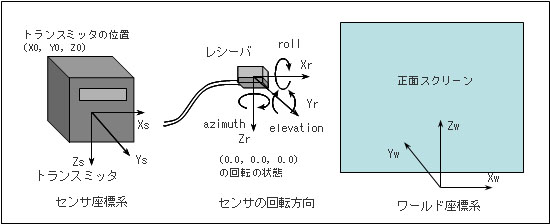
　　　　　　　　　　　　　　　　　　図9.3：Flock of Birdsのセンサ座標系

また、Flock of Birdsの姿勢を示す角度データは Azimuth, Elevation, Roll のオイラー角で表されます。そのため、トランスミッタのセンサ座標系の中でのレシーバの姿勢を求めるためには、レシーバの座標系（Xr, Yr, Zr）で示された方向ベクトルがセンサ座標系でどのように表されるか、ベクトルの変換の計算によって求めます。
レシーバの座標軸は下図のように、azimuth、elevation、roll の順に回転させることで姿勢を示しているため、これをセンサ座標にするには、roll、elevation、azimuth の逆の順番に回転変換の行列計算を行うことで求めることができます。

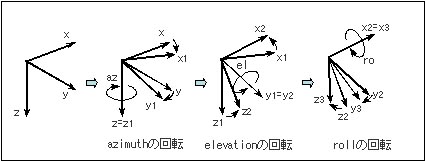
　　　　　　　　　　　　　　図9.4：オイラー角の回転

以下はレシーバ座標系でのベクトルをセンサ座標系のベクトルに変換するための行列計算です。行列計算の順番が逆になっていることに注意して下さい。

以上をもとに、センサ座標系の値をワールド座標系に変換する関数 spos_to_wpos(s_pos, w_pos)、レシーバ座標系のベクトルをセンサ座標系に変換する関数 rvec_to_svec(r_vec, ang, s_vec) を作成すると、以下のようになります。

　　float source_x = -1.0;　　/* ワールド座標系でのトランスミッタ位置 x (m) */
　　float source_y = 0.0;　　　/* ワールド座標系でのトランスミッタ位置 y (m) */
　　float source_z = 1.0;　　　/* ワールド座標系でのトランスミッタ位置 z (m) */

　　void spos_to_wpos(float s_pos[3], float w_pos[3])
　　/* s_pos：センサ座標系での位置(cm)、w_pos：ワールド座標系での位置(m) */
　　{
　　w_pos[0] = 0.0254*s_pos[0]+source_x;　　
　　w_pos[1] = -0.0254*s_pos[1]+source_y;
　　w_pos[2] = -0.0254*s_pos[2]+source_z;
　　return;
　　}

　　void matxvec(float mat[9], float vec[3], float ans[3])
　　{
　　ans[0] = mat[0]*vec[0]+mat[1]*vec[1]+mat[2]*vec[2];
　　ans[1] = mat[3]*vec[0]+mat[4]*vec[1]+mat[5]*vec[2];
　　ans[2] = mat[6]*vec[0]+mat[7]*vec[1]+mat[8]*vec[2];
　　return;
　　}

　　void rvec_to_svec(float r_vec[3], float ang[3], float s_vec[3])　　
　　 /* r_vec：レシーバ座標系でのベクトル、ang：オイラー角（degree）、s_vec：センサ座標系でのベクトル */
　　{
　　float angle[3];
　　float azimat[9], elemat[9], rolmat[9];
　　float tmp1vec[3], tmp2vec[3];

　　angle[0] = ang[0]/180.0*3.141592;　　　/* azimuth角度(radian) */
　　angle[1] = ang[1]/180.0*3.141592;　　　/* elevation角度(radian) */
　　angle[2] = ang[2]/180.0*3.141592;　　　/* roll角度(radian) */

　　azimat[0] = cos(angle[0]); 　　　/* azimuthの回転変換の行列の設定 */
　　azimat[1] = -sin(angle[0]);
　　azimat[2] = 0.0;
　　azimat[3] = sin(angle[0]);
　　azimat[4] = cos(angle[0]);
　　azimat[5] = 0.0;
　　azimat[6] = 0.0;
　　azimat[7] = 0.0;
　　azimat[8] = 1.0;

　　elemat[0] = cos(angle[1]); 　　　/* elevationの回転変換の行列の設定 */
　　elemat[1] = 0.0;
　　elemat[2] = sin(angle[1]);
　　elemat[3] = 0.0;
　　elemat[4] = 1.0;
　　elemat[5] = 0.0;
　　elemat[6] = -sin(angle[1]);
　　elemat[7] = 0.0;
　　elemat[8] = cos(angle[1]);

　　rolmat[0] = 1.0; 　　　　　　　　/* rollの回転変換の行列の設定 */
　　rolmat[1] = 0.0;
　　rolmat[2] = 0.0;
　　rolmat[3] = 0.0;
　　rolmat[4] = cos(angle[2]);
　　rolmat[5] =-sin(angle[2]);
　　rolmat[6] = 0.0;
　　rolmat[7] = sin(angle[2]);
　　rolmat[8] = cos(angle[2]);

　　matxvec(rolmat, r_vec, tmp1vec);　　　/* 回転変換の行列計算 */
　　matxvec(elemat, tmp1vec, tmp2vec);
　　matxvec(azimat, tmp2vec, s_vec);
　　return;
　　}

※演習：
上記の関数を実際に使用し、値がどう変わるか確認してみましょう。